Tutorial 23. Laurie Spiegel's Harmonic Algorithm and Entropy

An exploration of one of Laurie Spiegel's compositional programs as well as several of her other ideas.

Laurie Spiegel is one of the greats of computer music, composing in her early days at Bell Labs working with their GROOVE system (a microprocessor controlled analog synthesizer) and continuing to lead a prolific career creating both music and software for music.

In 2023, I was fortunate enough to see her present A Harmonic Algorithm: 2020, which is the latest iteration of a program she has been working on for several decades. An excerpt of an earlier version of the program is present on her album Unseen Worlds. I was deeply moved by this piece of music and in this tutorial we'll be diving into it as a fantastic case study in the beauty of computer music.

Much of this tutorial is drawn from Laurie's own words on her work. Several of her relevant papers have been downloaded from her website and archived here for convenience.

In particular, this tutorial will directly implement an approach described in Sonic Set Theory, so feel free to read her paper to see it explained in a more raw and artful way.

Laurie Spiegel's Harmonic Algorithm is an exploration of a destination-based generative approach to harmonic progressions. What I mean by destination-based is that there is a final landing point for the harmonic progression: in the simple case, the tonic of a scale. This algorithm could be applied to any harmonic grammar, but Laurie tests and presents it with a model derived from the music of J.S. Bach.

If you have taken a course or read a book covering classical music theory you have likely come across a diagram that looks like the following:

This (incomplete) diagram describes the "allowable" progressions of harmony within western pre-1800s classical music. Dominant leads to tonic, subdominant leads to dominant, etc. This somewhat regimented approach to harmony provides a good entrypoint for systematizing harmonic progression. Along the way, we will learn a few of Laurie's techniques for computationally working with tonality.

Non-linearity of sound and music

Many meaningful aspects of sound and music do not exhibit linearity.

A fundamental example of this is the octave. Suppose we have a 110Hz tone and we want to find the tone one octave up. We would double that frequency and find the next octave is at 220Hz, which is 110Hz higher than the previous octave. Now if we try to find the second octave up we can do the same thing, double the frequency again and find the second octave is at 440Hz. The difference here is that this octave is 220Hz higher than the previous octave, rather than 110Hz. You'll find that the higher pitch you get, the further apart (in Hz) these octaves get, though we perceive them as being equal. It turns out we perceive pitch exponentially rather than linearly!

How we divide the octave up into scales is typically non-linear as well. Take a major scale for example, it is made up of half steps and whole steps, distibuted unevenly. If we take it one step further, we don't use all scale degrees equally either. Tonic and dominant scale degrees typically appear in greater frequency than others. Leading tones tend to lead to tonics rather than fall to submediants. There are all sorts of inconsistencies to distribution in music.

Subsets and templates

The way that we tend to create and understand music is by creating subsets of greater sets of options. Let's explore how tonality emerges from the infinite possibilities of frequencies.

In this tutorial, we will be treating the 12-tone equal tempered (12TET) scale (specifically as defined by MIDI note numbers) as our fundamental set and building subsets on top of it.

We'll define a few useful templates. These are patterns we can overlay on top of a set create a useful subset from it:

Levels of indirection

We now have a nice numerical way for interacting with tonality so let's apply it to the common practice chord progression described above!

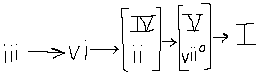
Laurie's model of this progression is in terms of what she calls "levels of indirection" from a destination chord (the tonic). Every chord will take some path that will eventually lead them to the tonic, and these chords can be described by how far away from the tonic they are. She describes this structure in terms of a tree (which should not be conflated with trees as a computer science concept) which must be descended one step at a time, moving from the leaves to the trunk. The parts of the tree are as follows:

Whichever level of the tree you are currently on, you are moving towards the trunk but must pass the in between levels on the way there.

This approach inherently gives a structure to your progression. Because there is always an end goal (the tonic) in sight, you will never find yourself lost in the recircling, aimless eddies that transition table appraches may create.

Entropy

Another useful concept which Laurie Spiegel introduces into algorithmic composition is entropy, which she borrows from the field of information theory.

Entropy can be defined as the amount of information (or uncertainty) contained within any musical event. She gives the example of a simple melody. The first time a melody is played, a listener has no idea what pitches (also rhythms, timbres, etc.) will be played so every note has a high amount of entropy. Each note is essentially giving you new information about the melody. This melody is pure information and lacks a lot of what makes music interesting: "conveying emotions through sameness and difference, anticipation, prediction, surprise, disappointment, reassurance, or return" in her words. If the melody is repeated, the results are musical; we are used to repetition. As it is continuously repeated, however, it becomes predictable and potentially boring. Every note is known before it is heard and the entropy level approaches zero as each note is slightly less meaningful (from an informational perspective) than the last.

fig 1. entropy decreasing as a melody is repeated over and over again

Because entropy is such an important part of our perception of music, it can be a useful tool for exercising higher order control over a composition. Imagine a generative system in which you as the composer have one large knob labelled entropy and nothing else. The system will generate music on its own that matches the entropy level of that knob. You would find that you have a great deal of control over the trajectory of the system's output. Turning just one knob could influence how hundreds of notes are played; you could create grand gradients of disorder to order, short bursts of chaos, long compositions of slowly mutating repetitions and who knows what else.

How this entropy arises could take many forms but a useful model is to thing of corruption events. A corruption event is a single event of chaos within an otherwise deterministic system. For example, if you are looping a simple melody, your corruption event could be playing a random chormatic note instead of whatever the next note of the melody would be. The more often this corruption event occurs, the more entropy there will be in this melody.

Defining corruption events this way gives us a lot of control over what this entropy sounds like. We aren't just generating pure white noise music; we can apply a set of rules to this event. Maybe instead of choosing a random chromatic note when a corruption happens, we could choose a random note from the key the melody is being played in. Or maybe instead of generating a random note, we could jump to a different note of our melody and continue from there. All of these options would increase the melody's entropy but have drastically different results.

Implementing Laurie Spiegel's Harmonic Algorithm on MEAP

In the remainder of this tutorial, we will be implementing a basic version of the above harmonic algorithm. We are just going to move from one chord to another, not worrying about arpeggiation, voice leading or anything like that. The discussion won't cover every line of code, but the full program is available at the bottom.

Our general approach will be that of a state machine:

We'll create the following variables to keep track of the current tree level and the current chord, respectively.

int tree_level = 4;  // what level of chord tree are we on
int chord_root = 2; // scale degree chord is built on, starting from 0

moving between tree levels

At regular points in time, perhaps once per second, we want to move on to the next tree level, simply decreasing the tree_level variable by one. Once we reach the bottom of the tree, we'll just jump up to a random level (from 0-4) and restart the process.

choosing chords

When we enter a new tree level, we'll also want to choose a chord to play. All levels except for #4 have two options of what chord to play for that level. We could arbitrarily choose one of those chords to always go to, but it would be more interesting to randomly choose one of the two chords to play. For example, on level #2 (the branches, chords with a subdominant function) we have the option to either play a IV or a ii chord. Let's arbitrarily choose to play the IV 66% of the time and ii 33% of the time. We could implement this as follows:

if (meap.irand(1, 100) > 33) {  // 66% change of IV, 33% chance of ii,
    chord_root = 3;               // IV chord (F major)
} else {
    chord_root = 1;               // ii chord (D minor)
}

We generate a random number between 1 and 100. If it is greater than 33 we play IV, if it is less than or equal to 33, we play ii.

applying templates to choose pitches

Now that we know what scale degree we want our chord to be based on, we can use Laurie's concepts of subsets and templates to choose the actual pitches to send to our oscillors. The following templates will help us out:

int major_scale[] = { 0, 2, 4, 5, 7, 9, 11 };  // template for building major scale on top of 12TET
int triad[] = { 0, 2, 4 };  // template for triad on top of major scale
int scale_root = 60;                           // root of major scale (arbitrarily chosen to be C3)

The scale_root variable lets us define the MIDI note number of the root of our scale, in this case we will choose it to be a C3 (MIDI note number 60). The major_scale template allows us to reference notes of a major scale in reference to this root. For example, if we wanted the midi note number of the 4th note (F) of a major scale built on this root:

scale_root + major_scale[3]

This also lets us easily build triads on top of the major scale without worrying about whether they need to be major, minor or diminished.

The triad template represents the scale degree offsets of each of the three notes of a triad (root, third and fifth). We can apply this to the major_scale template along with out chord_root variable defined above to easily get the MIDI note numbers of each note of our triad. The following line will find the MIDI note number of the root of a triad (given that you have defined a chord root as above).

scale_root + major_scale[chord_root + triad[0]

We can use this process to set the frequencies of our oscillators every time we move to a new chord:

osc1.setFreq(mtof(scale_root + major_scale[(triad[0] + chord_root) % 7]));      // root of chord (modded to octave)
osc2.setFreq(mtof(scale_root + major_scale[(triad[1] + chord_root) % 7]));      // third of chord (modded to octave)
osc3.setFreq(mtof(scale_root + major_scale[(triad[2] + chord_root) % 7]));      // fifth of chord (modded to octave)
osc4.setFreq(mtof(12 + scale_root + major_scale[(triad[0] + chord_root) % 7]));  // octave above root

The only weird thing in this block of code is the modulo %. Our template only covers one octave so if we tried to build a triad on the 7th scale degree, for example, we would have a problem because it would try to reference notes in the higher octave that aren't defined. The % 7 on each line will drop the octave of any notes that are higher than the top of our octave.

osc4 plays the frequency one octave up from our root by calculating in the same way and adding 12 to the MIDI note number.

The following code expands this process to cover all cases and plays the chords using four triangle wave voices.

An expanded version of this tutorial is located in the MEAP examples folder. It arpeggiates the chords and adds some entropy corruption events that will modify the order the chord is arpeggiated in and the envelopes of the notes.

FULL CODE BELOW

/*
  Implements a basic version of Laurie Spiegel's Harmonic Algorithm, changing chords every second.
 */

#define CONTROL_RATE 128  // Hz, powers of 2 are most reliable
#include <Meap.h>         // MEAP library, includes all dependent libraries, including all Mozzi modules

Meap meap;                                            // creates MEAP object to handle inputs and other MEAP library functions
MIDI_CREATE_INSTANCE(HardwareSerial, Serial1, MIDI);  // defines MIDI in/out ports

// ---------- YOUR GLOBAL VARIABLES BELOW ----------

// Synthesis
#include <tables/triangle_warm8192_int8.h>
mOscil<TRIANGLE_WARM8192_NUM_CELLS, AUDIO_RATE> osc1(TRIANGLE_WARM8192_DATA);
mOscil<TRIANGLE_WARM8192_NUM_CELLS, AUDIO_RATE> osc2(TRIANGLE_WARM8192_DATA);
mOscil<TRIANGLE_WARM8192_NUM_CELLS, AUDIO_RATE> osc3(TRIANGLE_WARM8192_DATA);
mOscil<TRIANGLE_WARM8192_NUM_CELLS, AUDIO_RATE> osc4(TRIANGLE_WARM8192_DATA);

ADSR<AUDIO_RATE, AUDIO_RATE> env1;
ADSR<AUDIO_RATE, AUDIO_RATE> env2;
ADSR<AUDIO_RATE, AUDIO_RATE> env3;
ADSR<AUDIO_RATE, AUDIO_RATE> env4;

// templates
int major_scale[] = { 0, 2, 4, 5, 7, 9, 11 };  // template for building major scale on top of 12TET
int scale_root = 60;                           // root of major scale

int triad[] = { 0, 2, 4 };  // template for triad on top of major scale
int chord_root = 2;         // root of triad

// chord timer
EventDelay chord_timer;
int chord_length = 1000;

int tree_level = 4;  // what level of chord tree are we on

void setup() {
  Serial.begin(115200);                      // begins Serial communication with computer
  Serial1.begin(31250, SERIAL_8N1, 43, 44);  // sets up MIDI: baud rate, serial mode, rx pin, tx pin
  startMozzi(CONTROL_RATE);                  // starts Mozzi engine with control rate defined above
  meap.begin();                              // sets up MEAP object

  // ---------- YOUR SETUP CODE BELOW ----------

  //set oscillators to pitches of first chord (iii chord on c major scale)
  osc1.setFreq(mtof(scale_root + major_scale[(triad[0] + chord_root) % 7]));
  osc2.setFreq(mtof(scale_root + major_scale[(triad[1] + chord_root) % 7]));
  osc3.setFreq(mtof(scale_root + major_scale[(triad[2] + chord_root) % 7]));
  osc4.setFreq(mtof(12 + scale_root + major_scale[(triad[0] + chord_root) % 7]));

  // sets envelope attack and sustain levels
  env1.setADLevels(255, 0);
  env2.setADLevels(255, 0);
  env3.setADLevels(255, 0);
  env4.setADLevels(255, 0);

  // sets envelope times
  env1.setTimes(1, 500, 1, 1);
  env2.setTimes(1, 500, 1, 1);
  env3.setTimes(1, 500, 1, 1);
  env4.setTimes(1, 500, 1, 1);
}


void loop() {
  audioHook();  // handles Mozzi audio generation behind the scenes
}


/** Called automatically at rate specified by CONTROL_RATE macro, most of your mode should live in here
	*/
void updateControl() {
  meap.readInputs();
  // ---------- YOUR updateControl CODE BELOW ----------
  if (chord_timer.ready()) {

    // move to next tree level
    if (tree_level != 0) {  // move one level down tree
      tree_level = tree_level - 1;
    } else {  // if at bottom of tree (0), jump to a random level
      tree_level = meap.irand(0, 4);
    }

    // choose chord depending on current level
    switch (tree_level) {
      case 4:            // leaves: iii
        chord_root = 2;  // iii chord (E minor)
        break;
      case 3:                           // twigs: I or vi
        if (meap.irand(1, 100) > 25) {  // 25% chance of I, 75% chance of vi
          chord_root = 5;               // vi chord (A minor)
        } else {
          chord_root = 0;  // I chord (C major)
        }
        break;
      case 2:                           // branches: IV or ii
        if (meap.irand(1, 100) > 33) {  // 66% change of IV, 33% chance of ii
          chord_root = 3;               // IV chord (F major)
        } else {

          chord_root = 1;  // ii chord (D minor)
        }
        break;
      case 1:// boughs: V or vii˚
        if (meap.irand(1, 100) > 25) {  // 75% change of V, 25% chance of vii˚
          chord_root = 4;               // V chord (G major)
        } else {
          chord_root = 6;  // vii˚ chord (B diminished)
        }
        break;
      case 0:                 // trunk: I or vi
        if (meap.irand(1, 100) > 25) { // 75% change of I, 25% chance of vi
          chord_root = 0;  // I chord (C major)
        } else {
          chord_root = 5;  // vi chord (A minor)
        }
        break;
    }

    // set oscillator frequencies
    osc1.setFreq(mtof(scale_root + major_scale[(triad[0] + chord_root) % 7]));      // root of chord (modded to octave)
    osc2.setFreq(mtof(scale_root + major_scale[(triad[1] + chord_root) % 7]));      // third of chord (modded to octave)
    osc3.setFreq(mtof(scale_root + major_scale[(triad[2] + chord_root) % 7]));      // fifth of chord (modded to octave)
    osc4.setFreq(2 * mtof(scale_root + major_scale[(triad[0] + chord_root) % 7]));  // octave above root

    // trigger all notes
    env1.noteOn();
    env2.noteOn();
    env3.noteOn();
    env4.noteOn();

    // start timer
    chord_timer.start(chord_length);
  }
}

/** Called automatically at rate specified by AUDIO_RATE macro, for calculating samples sent to DAC, too much code in here can disrupt your output
	*/
AudioOutput_t updateAudio() {
  env1.update();
  env2.update();
  env3.update();
  env4.update();

  int64_t out_sample = osc1.next() * env1.next() + osc2.next() * env2.next() + osc3.next() * env3.next() + osc4.next() * env4.next();

  return StereoOutput::fromNBit(18, (out_sample * meap.volume_val) >> 12, (out_sample * meap.volume_val) >> 12);
}

/**
   * Runs whenever a touch pad is pressed or released
   *
   * int number: the number (0-7) of the pad that was pressed
   * bool pressed: true indicates pad was pressed, false indicates it was released
   */
void updateTouch(int number, bool pressed) {
  if (pressed) {  // Any pad pressed

  } else {  // Any pad released
  }
  switch (number) {
    case 0:
      if (pressed) {  // Pad 0 pressed
        Serial.println("t0 pressed ");
      } else {  // Pad 0 released
        Serial.println("t0 released");
      }
      break;
    case 1:
      if (pressed) {  // Pad 1 pressed
        Serial.println("t1 pressed");
      } else {  // Pad 1 released
        Serial.println("t1 released");
      }
      break;
    case 2:
      if (pressed) {  // Pad 2 pressed
        Serial.println("t2 pressed");
      } else {  // Pad 2 released
        Serial.println("t2 released");
      }
      break;
    case 3:
      if (pressed) {  // Pad 3 pressed
        Serial.println("t3 pressed");
      } else {  // Pad 3 released
        Serial.println("t3 released");
      }
      break;
    case 4:
      if (pressed) {  // Pad 4 pressed
        Serial.println("t4 pressed");
      } else {  // Pad 4 released
        Serial.println("t4 released");
      }
      break;
    case 5:
      if (pressed) {  // Pad 5 pressed
        Serial.println("t5 pressed");
      } else {  // Pad 5 released
        Serial.println("t5 released");
      }
      break;
    case 6:
      if (pressed) {  // Pad 6 pressed
        Serial.println("t6 pressed");
      } else {  // Pad 6 released
        Serial.println("t6 released");
      }
      break;
    case 7:
      if (pressed) {  // Pad 7 pressed
        Serial.println("t7 pressed");
      } else {  // Pad 7 released
        Serial.println("t7 released");
      }
      break;
  }
}

/**
   * Runs whenever a DIP switch is toggled
   *
   * int number: the number (0-7) of the switch that was toggled
   * bool up: true indicated switch was toggled up, false indicates switch was toggled
   */
void updateDip(int number, bool up) {
  if (up) {  // Any DIP toggled up

  } else {  //Any DIP toggled down
  }
  switch (number) {
    case 0:
      if (up) {  // DIP 0 up
        Serial.println("d0 up");
      } else {  // DIP 0 down
        Serial.println("d0 down");
      }
      break;
    case 1:
      if (up) {  // DIP 1 up
        Serial.println("d1 up");
      } else {  // DIP 1 down
        Serial.println("d1 down");
      }
      break;
    case 2:
      if (up) {  // DIP 2 up
        Serial.println("d2 up");
      } else {  // DIP 2 down
        Serial.println("d2 down");
      }
      break;
    case 3:
      if (up) {  // DIP 3 up
        Serial.println("d3 up");
      } else {  // DIP 3 down
        Serial.println("d3 down");
      }
      break;
    case 4:
      if (up) {  // DIP 4 up
        Serial.println("d4 up");
      } else {  // DIP 4 down
        Serial.println("d4 down");
      }
      break;
    case 5:
      if (up) {  // DIP 5 up
        Serial.println("d5 up");
      } else {  // DIP 5 down
        Serial.println("d5 down");
      }
      break;
    case 6:
      if (up) {  // DIP 6 up
        Serial.println("d6 up");
      } else {  // DIP 6 down
        Serial.println("d6 down");
      }
      break;
    case 7:
      if (up) {  // DIP 7 up
        Serial.println("d7 up");
      } else {  // DIP 7 down
        Serial.println("d7 down");
      }
      break;
  }
}