Tutorial 22. Transition Tables
| Analysis-based automatic melody generation. |
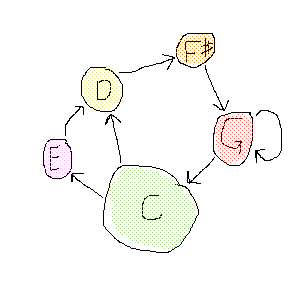 |
When designing a system that automatically generates a melody, we typically have a set of expectations for that melody. We may want it to be in a certain key signature, have a certain style (distribution of melodic intervals and rhythms), etc. You could attempt to encode all of these expectations into a set of rules like the rules for setting counterpoint, but depending on your goals, this could become impractical. You may find it more fruitful to do some sort of data analysis on a hand-crafted melody in the style that you are interested in, and model your melody after this analysis.
In this tutorial, we will an explore a primitive approach to this, the first-order transition table, and apply it to the classic song, Happy Birthday.

The goal of a transition table is to describe the probability of certain events following other events. You can define these events as whatever you want them to be but we'll start with the simplest case: defining them as pitches. A pitch transition table should tell us, for example, if the current note is a C, what is the probability that the next note is a D (or an E, or a Bb, etc)
In the example of Happy Birthday, we will derive this transition table by looking at each note within the sheet music, looking at the note that follows it and adding this as a tally in a table. If you count it up, when a C occurs in the sheet music, it is followed by another C three times, a D twice, an F once, a G once, and a high C (notated as C^) once. What this tells us is that if we want to generate a melody that sounds like Happy Birthday, Cs should often be followed by more Cs, never be followed by a Bb, sometimes be followed by a G, etc. Repeat this process for every note and we now have a probabilistic model of which notes will follow each other in this song!
Note transition table:
| Next note | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| C u r r e n t N o t e |
|
Now that we have this analysis, how could we generate a new melody that matches these probabilities? Well, if we look at the C row, and count up all of the occurences of subsequent notes, there are 8 of them. From this we can surmise that there is a 3/8 chance of a C being followed by another C, a 2/8 chance of a C being followed by a D, etc. So maybe we can pull out a set of Dungeons and Dragons dice, roll our eight-sided die, and make the following ruleset:
Given our current note is C, roll an eight-sided die to choose the next note:
- 1, 2 or 3 mean the next note is C
- 4 or 5 mean the next note is D
- 6 means the next note is F
- 7 means the next note is G
- 8 means the next note is C^
This will work great, but when we try we do the same process for the D row, well, there are only three occurences here so it looks like we'll need a three-sided die. And a five sided-die for the F row. It would be great if we could find a way to standardize this process!
It turns out what we did with the eight-sided die was the first step towards creating what, in the world of probability theory, is called a Cumulative Distribution Function, albeit in a somewhat weird form.
The first step to standardizing our calculation of next note is to normalize our transition table so that each row adds up to exactly 1. This will make each box represent a probability in the classical sense (from 0 to 1) of that note occuring next. To do this we will add up all the entries in each row, and divide that row by the total. So for the C row, we'll be dividing each number by 8.
Normalized note transition table:
| Next note | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| C u r r e n t N o t e |
|
Now everything is nicely normalized to the same range. Every row will perfectly add up to 1 when summed together. But there's still not a great way to use a random number generator to select the next note. What we want to do is generate a random number between 0 and 1 and depending on the result, choose the next note. The easiest way to do this is to set up ranges just like we did on our eight-sided die!
For the C row, generate a number N between 0 and 1:
- if N >= 0 and N < 0.375, the next note is C
- if N >= 0.375 and N < 0.625, the next note is E
- if N >= 0.625 and N < 0.75, the next note is F
- if N >= 0.75 and N < 0.875, the next note is G
- if N >= 0.875 and N <= 1.0, the next note is C^
For convenience, we can derive the following table by cumulatively adding cells from left to right along each row.
Cumultive note transition table:
| Next note | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| C u r r e n t N o t e |
|
This table is a little unintuitive to read but it will make it easier for us to implement this in code. We can use the following algorithm to choose the next note given the current one.
- Locate the row corresponding to current note.
- Generate a random number between zero and one.
- Starting at the left-most cell, is the random number
less than the number in the cell?
- if yes, the next note is the one corresponding to the column you are currently in.
- if no, move right one cell and ask the same question. Repeat until yes.
We can create transition tables for any other musical parameters. In this case we'll just create one more for rhythms. We could take the same approach we did with pitches by treating each note as our event of interest, but we may get more interesting results if we choose a slightly higher level event. We are going to treat the rhythm of each measure as an event and string these together.
You'll notice that there are only three distinct rhythms present in this song:
- rhythm 0: quarter note, quarter note, quarter note
- rhythm 1: half note, dotted eighth note, sixteenth note
- rhythm 2: quarter note, quarter note, dotted eighth note, sixteenth note
We'll treat the pickup note and final incomplete measure as parts of the same measure which will cycle around from end to beginning as if the song was repeating. The following cumulative transition table arises from this analysis:
Cumultive rhythm transition table:
| Next rhythm | |||||||||||||||||
| C R u h r y r t e h n m t |
|
The following code implements both of these transition tables, continuously generating a melody that is statistically similar to Happy Birthday. You will notice that on a note-to-note basis, it is coherent. All of the intervals played make sense and occur in Happy Birthday. If you pay attention to more than a few notes in a row, the model seems to break down a bit though. Melodies seem to go nowhere, looping or terminating early. Rhythms don't seem to match up with the pitches they would be correlated with in the real song and it is rare to reach any satisfying finality. The main cause of all of this, is that this is only a first-order transition table. Our statistical analysis only ties every event to the event directly before and after it, and none of the higher-order structure order of the melody was captured. To solve this, you could perhaps create a second-order transition table, where the next pitch to be played depends not only on the current note, but the note that preceded it as well. Now you would have a three-note chain of coherence instead of just two. But, no matter how high-order you make your transition table, there will always be one more step back that is not captured by it.
The unavoidable fact of transition tables is that, while they are great at providing low-order, note-to-note coherency, they aren't great at capturing higher-order musical features like the full contour of a melody, or sections of a piece of music. Other methods would need to be taken to capture these.
A final note is that transition tables don't need to arise
from analysing a corpus of music. You could also hand-pick a
set of probabilities (or derive them from some other
source) that you think would be interesting and see what
results it gives you. Feel free to mess with the numbers in
note_transition and
rhythm_transition in the code below, maybe it
will create a fantastic melody!
FULL CODE BELOW
/*
Implements a first-order transition table-based recreation of the classic song "happy birthday"
Separate transition tables are used to model first-order pitch sequences and measure-to-measure rhythm sequences
*/
#define CONTROL_RATE 128 // Hz, powers of 2 are most reliable
#include <Meap.h> // MEAP library, includes all dependent libraries, including all Mozzi modules
Meap meap; // creates MEAP object to handle inputs and other MEAP library functions
MIDI_CREATE_INSTANCE(HardwareSerial, Serial1, MIDI); // defines MIDI in/out ports
// ---------- YOUR GLOBAL VARIABLES BELOW ----------
#include <tables/triangle_warm8192_int8.h>
mOscil<TRIANGLE_WARM8192_NUM_CELLS, AUDIO_RATE> osc(TRIANGLE_WARM8192_DATA);
ADSR<CONTROL_RATE, AUDIO_RATE> env;
// for triggering the envelope
EventDelay note_delay;
int sixteenth_length = 100;
#define NUM_NOTES 8
int note_pitches[] = { 60, 62, 64, 65, 67, 69, 70, 72 }; // list of pitches used in each row of transition table
float note_transition[NUM_NOTES][NUM_NOTES] = // tally of number of occurences of each note transition
{
{ 3, 2, 0, 1, 1, 0, 0, 1 }, //from C
{ 2, 0, 0, 0, 0, 0, 1, 0 }, //from D
{ 2, 0, 0, 0, 0, 0, 1, 0 }, //from E
{ 1, 0, 2, 0, 1, 0, 0, 0 }, //from f
{ 0, 0, 0, 2, 0, 0, 0, 0 }, //from G
{ 0, 0, 0, 2, 0, 0, 0, 0 }, //from A
{ 0, 0, 0, 0, 0, 1, 1, 0 }, //from Bb
{ 0, 0, 0, 0, 1, 0, 0, 0 }, //from C^
};
float note_transition_cumulative[NUM_NOTES][NUM_NOTES] = // in setup we will convert the above transition table to cumulative distribution function
{
{ 0, 0, 0, 0, 0, 0, 0, 0 }, //from C
{ 0, 0, 0, 0, 0, 0, 0, 0 }, //from D
{ 0, 0, 0, 0, 0, 0, 0, 0 }, //from E
{ 0, 0, 0, 0, 0, 0, 0, 0 }, //from f
{ 0, 0, 0, 0, 0, 0, 0, 0 }, //from G
{ 0, 0, 0, 0, 0, 0, 0, 0 }, //from A
{ 0, 0, 0, 0, 0, 0, 0, 0 }, //from Bb
{ 0, 0, 0, 0, 0, 0, 0, 0 }, //from C^
};
int curr_note = 0;
// Transition table for rhythms on a measure-wide basis
// 0: q q q
// 1: h e. s
// 2: q q e. s
#define NUM_RHYTHMS 3
float rhythm_transition[3][3] = {
{ 0, 3, 1 }, // from 0: q q q
{ 3, 0, 0 }, // from 1: h e. s
{ 1, 0, 0 }, // from 2: q q e. s
};
float rhythm_cumulative[3][3] = {
{ 0, 0, 0},
{ 0, 0, 0},
{ 0, 0, 0},
};
int current_rhythm; // rhythm currently playing
int rhythm_queue[4] = { 0 }; // queue of note lengths to play (max of 4 because longest rhythm is 4 notes)
int rhythm_length; // length of current rhythm
int rhythm_index; // what note within current rhythm are we playing
void setup() {
Serial.begin(115200); // begins Serial communication with computer
Serial1.begin(31250, SERIAL_8N1, 43, 44); // sets up MIDI: baud rate, serial mode, rx pin, tx pin
startMozzi(CONTROL_RATE); // starts Mozzi engine with control rate defined above
meap.begin(); // sets up MEAP object
// ---------- YOUR SETUP CODE BELOW ----------
env.setADLevels(255, 200); // set attack level to maximum, and sustain level slightly lower
env.setTimes(1, 100, 0, 500);
// ---------- CALCULATING NOTE TRANSITION TABLE ----------
int note_sums[] = { 0, 0, 0, 0, 0, 0, 0, 0 };
// CALCULATING SUMS
for (int row = 0; row < NUM_NOTES; row++) {
for (int col = 0; col < NUM_NOTES; col++) {
note_sums[row] += note_transition[row][col];
}
}
// NORMALIZING PDF
for (int row = 0; row < NUM_NOTES; row++) {
for (int col = 0; col < NUM_NOTES; col++) {
note_transition[row][col] /= note_sums[row];
}
}
// CALCULATING CUMULATIVE PDF
for (int row = 0; row < NUM_NOTES; row++) {
for (int col = 0; col < NUM_NOTES; col++) { // compute cumulative probability density function
for (int i = 0; i <= col; i++) {
note_transition_cumulative[row][col] += note_transition[row][i];
}
}
}
// ------CALCULATING RHYTHM TRANSITION TABLE-------
// SETTING UP PROBABILITY DENSITY FUNCTION
int rhythm_sums[NUM_RHYTHMS] = { 0 };
// CALCULATING SUMS
for (int row = 0; row < NUM_RHYTHMS; row++) {
for (int col = 0; col < NUM_RHYTHMS; col++) {
rhythm_sums[row] += rhythm_transition[row][col];
}
}
// NORMALIZING PDF
for (int row = 0; row < NUM_RHYTHMS; row++) {
for (int col = 0; col < NUM_RHYTHMS; col++) {
rhythm_transition[row][col] /= rhythm_sums[row];
}
}
// CALCULATING CUMULATIVE PDF
for (int row = 0; row < NUM_RHYTHMS; row++) {
for (int col = 0; col < NUM_RHYTHMS; col++) { // compute cumulative probability density function
for (int i = 0; i <= col; i++) {
rhythm_cumulative[row][col] += rhythm_transition[row][i];
}
}
}
// initialize first rhythm
rhythm_queue[0] = 4 * sixteenth_length;
rhythm_queue[1] = 4 * sixteenth_length;
rhythm_queue[2] = 4 * sixteenth_length;
rhythm_length = 3;
rhythm_index = 0;
note_delay.start(rhythm_queue[0]);
env.noteOn();
osc.setFreq(mtof(note_pitches[curr_note]));
}
void loop() {
audioHook(); // handles Mozzi audio generation behind the scenes
}
/** Called automatically at rate specified by CONTROL_RATE macro, most of your mode should live in here
*/
void updateControl() {
meap.readInputs();
// ---------- YOUR updateControl CODE BELOW ----------
if (note_delay.ready()) { // silent night
//move to next pitch
float R = meap.frand();
for (int i = 0; i < 8; i++) {
if (note_transition_cumulative[curr_note][i] >= R) {
curr_note = i;
break;
}
}
osc.setFreq(mtof(note_pitches[curr_note])); //set frequency of sine oscillator
env.noteOn();
rhythm_index++;
if (rhythm_index >= rhythm_length) { //reached end of current rhythm
rhythm_index = 0;
float R = meap.frand();
for (int i = 0; i < NUM_RHYTHMS; i++) {
if (rhythm_cumulative[current_rhythm][i] >= R) {
current_rhythm = i;
break;
}
}
switch (current_rhythm) {
case 0: // q q q
rhythm_queue[0] = 4 * sixteenth_length;
rhythm_queue[1] = 4 * sixteenth_length;
rhythm_queue[2] = 4 * sixteenth_length;
rhythm_length = 3;
break;
case 1: // h e. s
rhythm_queue[0] = 8 * sixteenth_length;
rhythm_queue[1] = 3 * sixteenth_length;
rhythm_queue[2] = 1 * sixteenth_length;
rhythm_length = 3;
break;
case 2: // q q e. s
rhythm_queue[0] = 4 * sixteenth_length;
rhythm_queue[1] = 4 * sixteenth_length;
rhythm_queue[2] = 3 * sixteenth_length;
rhythm_queue[3] = sixteenth_length;
rhythm_length = 4;
break;
}
}
note_delay.start(rhythm_queue[rhythm_index]);
}
env.update();
}
/** Called automatically at rate specified by AUDIO_RATE macro, for calculating samples sent to DAC, too much code in here can disrupt your output
*/
AudioOutput_t updateAudio() {
int64_t out_sample = osc.next() * env.next();
return StereoOutput::fromNBit(16, (out_sample * meap.volume_val) >> 12, (out_sample * meap.volume_val) >> 12);
}
/**
* Runs whenever a touch pad is pressed or released
*
* int number: the number (0-7) of the pad that was pressed
* bool pressed: true indicates pad was pressed, false indicates it was released
*/
void updateTouch(int number, bool pressed) {
if (pressed) { // Any pad pressed
} else { // Any pad released
}
switch (number) {
case 0:
if (pressed) { // Pad 0 pressed
Serial.println("t0 pressed ");
} else { // Pad 0 released
Serial.println("t0 released");
}
break;
case 1:
if (pressed) { // Pad 1 pressed
Serial.println("t1 pressed");
} else { // Pad 1 released
Serial.println("t1 released");
}
break;
case 2:
if (pressed) { // Pad 2 pressed
Serial.println("t2 pressed");
} else { // Pad 2 released
Serial.println("t2 released");
}
break;
case 3:
if (pressed) { // Pad 3 pressed
Serial.println("t3 pressed");
} else { // Pad 3 released
Serial.println("t3 released");
}
break;
case 4:
if (pressed) { // Pad 4 pressed
Serial.println("t4 pressed");
} else { // Pad 4 released
Serial.println("t4 released");
}
break;
case 5:
if (pressed) { // Pad 5 pressed
Serial.println("t5 pressed");
} else { // Pad 5 released
Serial.println("t5 released");
}
break;
case 6:
if (pressed) { // Pad 6 pressed
Serial.println("t6 pressed");
} else { // Pad 6 released
Serial.println("t6 released");
}
break;
case 7:
if (pressed) { // Pad 7 pressed
Serial.println("t7 pressed");
} else { // Pad 7 released
Serial.println("t7 released");
}
break;
}
}
/**
* Runs whenever a DIP switch is toggled
*
* int number: the number (0-7) of the switch that was toggled
* bool up: true indicated switch was toggled up, false indicates switch was toggled
*/
void updateDip(int number, bool up) {
if (up) { // Any DIP toggled up
} else { //Any DIP toggled down
}
switch (number) {
case 0:
if (up) { // DIP 0 up
Serial.println("d0 up");
} else { // DIP 0 down
Serial.println("d0 down");
}
break;
case 1:
if (up) { // DIP 1 up
Serial.println("d1 up");
} else { // DIP 1 down
Serial.println("d1 down");
}
break;
case 2:
if (up) { // DIP 2 up
Serial.println("d2 up");
} else { // DIP 2 down
Serial.println("d2 down");
}
break;
case 3:
if (up) { // DIP 3 up
Serial.println("d3 up");
} else { // DIP 3 down
Serial.println("d3 down");
}
break;
case 4:
if (up) { // DIP 4 up
Serial.println("d4 up");
} else { // DIP 4 down
Serial.println("d4 down");
}
break;
case 5:
if (up) { // DIP 5 up
Serial.println("d5 up");
} else { // DIP 5 down
Serial.println("d5 down");
}
break;
case 6:
if (up) { // DIP 6 up
Serial.println("d6 up");
} else { // DIP 6 down
Serial.println("d6 down");
}
break;
case 7:
if (up) { // DIP 7 up
Serial.println("d7 up");
} else { // DIP 7 down
Serial.println("d7 down");
}
break;
}
}