Tutorial 12. Wavetables, sampling, and a piano sound
| In which play a piano and explore an example of how all knowledge is the same. |
 |
Our goal in this tutorial is to play back recorded samples of a piano using our touch keyboard, but first let's dive into how sampling works and how it is very closely related to our mOscil class!
The job of an simple oscillator is to play an unchanging waveform. The pitch may change, but the fundamental waveform being created by the oscillator shouldn't; a saw wave oscillator should always play a saw wave.
Try to imagine an algorithm for mathematically generating an 8-bit saw wave. It's not too difficult:
- Start with a value at 127
- Gradually decrease this value at a rate that corresponds to your desired frequency.
- When you reach -128, reset back down to 127 and repeat.
You can probably come up with similar algorithms to generate a square wave, triangle wave and, if you have a way to calculate trigonometric functions, a sine wave as well. What if we wanted to generate the following waveform though:
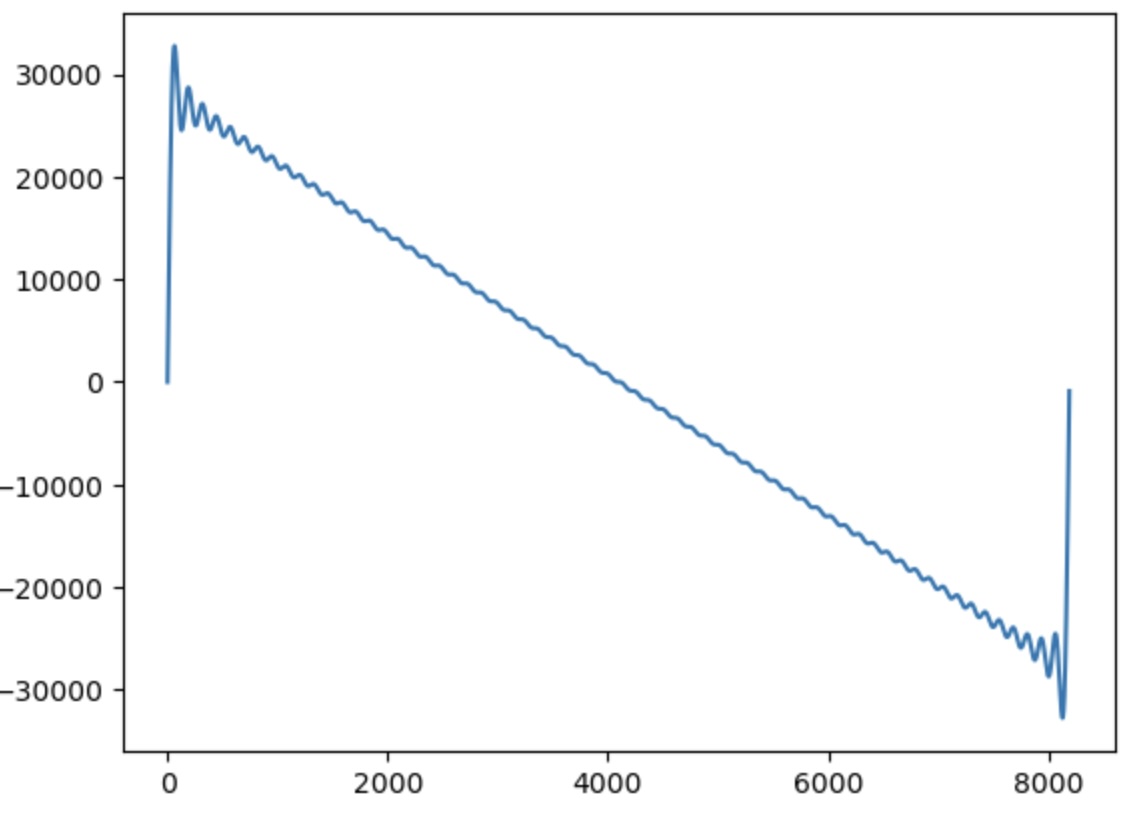fig 1. graph of saw8192_int16.h from the Meap library
This is a graph of a bandlimited sawtooth wave (which happens to be the waveform we used in tutorial 8.) Band-limited waveforms are ubiquitous in digital synthesis. A perfect, non-bandlimited sawtooth wave has harmonics at every integer multiple of the fundamental frequency, going all the way up to infinity. If we tried to play this wave in a digital system we would run into a problem. According to the Nyquist-Shannon Sampling Theorem, a digital system can only represent frequencies up to half the sampling rate. If you try to play higher frequencies, they will alias and cause potentially audible artifacts, which is exactly what will happen in the case of our perfect sawtooth wave. The solution is to use a band-limited waveform, which is an imperfect version of a desired waveform thats cuts off all frequencies above a certain value, eliminating the frequencies that would alias.
Now try to imagine an algorithm to generate this waveform; it's a lot more difficult. This waveform in specific was generated by adding together 64 sine wave harmonics, meaning to calculate this one waveform, we need to evaluate 64 sin functions per sample! You could also bandlimit a waveform by generating a non-bandlimited waveform and applying a lowpass filter to it, but either way it gets significantly more computationally intensive.
Going back to to the goal of our oscillator, we really just want it to generate the same waveform over and over again, so it turns out a lot of these calculations are superfluous. What if we could calculate just one cycle of this waveform and play it over and over again? Well, the result would be exactly the same, and that is how a lot of digital oscillators are implemented. We call this single pre-calculated cycle a wavetable and the oscillator that uses it, a wavetable oscillator
You'll remember that when we create an mOscil, there are a few things we need to tell it.
- NUM_TABLE_CELLS: This tells us how many samples long this wavetable is. The more samples, the higher the resolution.
- TABLE_NAME: This points the oscillator to the data of the wavetable itself, which is stored as an array in memory.
The important thing to remember is that this wavetable is just a series of numbers that represent the sample-by-sample amplitude of a wave over time. To play this wavetable as an oscillator, we sequentially move through these numbers and send them to the DAC. If we play through these numbers one after the other, the pitch that we hear will depend both on the size of the wavetable, and our sampling rate. If our wavetable has 8192 samples, and our sampling rate is 32768Hz we can play the wavetable four times in one second (8192 / 32768 = 4) resulting in a 4Hz tone, which is, of course, too low of a frequency for us to percieve as a tone. Imagine, however, instead of playing every sample in this wavetable, we played every other sample. Now we can move through the wavetable twice as fast, fitting eight wavetables into one second and we have increased our pitch to 8Hz. You can think of it like playing a 33rpm record at 45rpm, we move through the sound more quickly so it gets pitched up. This principle will allow us to play the wavetable at any pitch, we just need to choose how many samples to skip (or to play multiple times if we want a lower pitch) to get us to our desired frequency. That number can be calculated using the following formula.
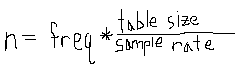
Using this idea, we can now store a wavetable of arbitrary shape in memory and play it at any frequency!
It turns out, this process is also exactly how samplers work! We store a sample (such as a recording of a piano playing a note) in memory as a table, and play it back. A sampler, is fundamentally just a wavetable oscillator.
The main difference is that samplers typically work with larger tables. A two second recording of a piano playing a note stored with a sampling rate of 32768Hz will have 65536 samples in comparison to the mere 8192 of our wavetable oscillator. Also, while a wavetable oscillator plays through the wavetable repeatedly to generate a sound, you may be happy with a sampler that just plays the sample once from front to back.
The mSample object (which is a rewriting of the Mozzi Sample object which overcomes some of its limitations) implements a sampler in this manner. If you look at the code underlying it, it is almost identical to the mOscil object.
There are a few things to do when using the mSample object.
-
Setting up the object is exactly the same as setting up an oscillator. We need to tell it how big the table is, whether you want to play it at audio rate or control rate (this will almost always be audio rate), tell it if the sample is 16 bits and finally point it to the data array. We're using a sample included with the Meap library of a piano playing a C.
#include "tables/Glass_Piano_C.h" mSample<Glass_Piano_C_NUM_CELLS, AUDIO_RATE, int16_t> my_sample(Glass_Piano_C_DATA); -
Next is setting the frequency of the sample. We can't set the frequency the same way we do for an oscillator. mSample doesn't know if the sample you loaded into memory contains a recording of a piano playing a C, playing a D, or even a non-pitched sound, so frequency doesn't mean much for us here. Instead, we want to think about how fast to play through the sample in relation to the speed it was recorded at. If we want to play at the same speed it was recorded, we divide the sample rate by the length of the sample. Since our result will be a fractional value, we need to convert these numbers to floats first by casting them.
default_freq = (float)Glass_Piano_C_SAMPLERATE / (float)Glass_Piano_C_NUM_CELLS; my_sample.setFreq(default_freq); // play at the speed it was recordedIn this case, we want the touch keyboard to re-pitch this sample to the notes of a C major scale. To do this, we need to know the frequency ratios of the intervals we want (minor second, major second, minor third, etc.) Assuming we are using 12-tone equal temperament as our tuning system, the frequency ratio between a note and another note n semitones away can be calculated as follows:
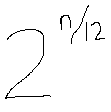
This formula works for negative values of n as well (pitching down your sample rather than up)
In the updateTouch function, we evaluate this formula for all the intervals of a major scale in semitones (0, 2, 4, 5, 7, 9, 11, 12)
-
Finally we need to tell the sample to start! The
start()method will play the sample once through from beginning to end. Note that it doesn't continuously loop like a wavetable oscillator does, (but if we wanted it to we could call the setLoopingOn() method somewhere in your code and then it would loop back to the beginning every time the end of the sample was reached). In this case we call thestart()method every time a touch pad is pressed.
Upload the following code, press some pads and you should hear a piano sound!
Try replacing the piano sample with your own sounds. The first script on the meapscripts page will convert any audio file you give it into a MEAP compatible sample array so go ahead and convert something, rename the variables in your code and reupload. Note that there is a limit to the memory on MEAP so trying to load samples longer than a minute or so (especially if they are 16-bit samples) may not work.
FULL CODE BELOW
/*
Basic template for working with a stock MEAP board.
*/
#define CONTROL_RATE 128 // Hz, powers of 2 are most reliable
#include <Meap.h> // MEAP library, includes all dependent libraries, including all Mozzi modules
Meap meap; // creates MEAP object to handle inputs and other MEAP library functions
MIDI_CREATE_INSTANCE(HardwareSerial, Serial1, MIDI); // defines MIDI in/out ports
// ---------- YOUR GLOBAL VARIABLES BELOW ----------
#include "tables/Glass_Piano_C.h"
// variables for sample
mSample<Glass_Piano_C_NUM_CELLS, AUDIO_RATE, int16_t> my_sample(Glass_Piano_C_DATA);
float default_freq;
void setup() {
Serial.begin(115200); // begins Serial communication with computer
Serial1.begin(31250, SERIAL_8N1, 43, 44); // sets up MIDI: baud rate, serial mode, rx pin, tx pin
startMozzi(CONTROL_RATE); // starts Mozzi engine with control rate defined above
meap.begin(); // sets up MEAP object
// ---------- YOUR SETUP CODE BELOW ----------
default_freq = (float)Glass_Piano_C_SAMPLERATE / (float)Glass_Piano_C_NUM_CELLS;
my_sample.setFreq(default_freq); // play at the speed it was recorded
}
void loop() {
audioHook(); // handles Mozzi audio generation behind the scenes
}
/** Called automatically at rate specified by CONTROL_RATE macro, most of your mode should live in here
*/
void updateControl() {
meap.readInputs();
// ---------- YOUR updateControl CODE BELOW ----------
}
/** Called automatically at rate specified by AUDIO_RATE macro, for calculating samples sent to DAC, too much code in here can disrupt your output
*/
AudioOutput_t updateAudio() {
int64_t out_sample = my_sample.next();
return StereoOutput::fromNBit(16, (out_sample * meap.volume_val) >> 12, (out_sample * meap.volume_val) >> 12);
}
/**
* Runs whenever a touch pad is pressed or released
*
* int number: the number (0-7) of the pad that was pressed
* bool pressed: true indicates pad was pressed, false indicates it was released
*/
void updateTouch(int number, bool pressed) {
if (pressed) { // Any pad pressed
} else { // Any pad released
}
switch (number) {
case 0:
if (pressed) { // Pad 0 pressed
Serial.println("t0 pressed ");
my_sample.setFreq(default_freq);
my_sample.start();
} else { // Pad 0 released
Serial.println("t0 released");
}
break;
case 1:
if (pressed) { // Pad 1 pressed
Serial.println("t1 pressed");
my_sample.setFreq(default_freq * pow(2, 2.0 / 12.0));
my_sample.start();
} else { // Pad 1 released
Serial.println("t1 released");
}
break;
case 2:
if (pressed) { // Pad 2 pressed
Serial.println("t2 pressed");
my_sample.setFreq(default_freq * pow(2, 4.0 / 12.0));
my_sample.start();
} else { // Pad 2 released
Serial.println("t2 released");
}
break;
case 3:
if (pressed) { // Pad 3 pressed
Serial.println("t3 pressed");
my_sample.setFreq(default_freq * pow(2, 5.0 / 12.0));
my_sample.start();
} else { // Pad 3 released
Serial.println("t3 released");
}
break;
case 4:
if (pressed) { // Pad 4 pressed
Serial.println("t4 pressed");
my_sample.setFreq(default_freq * pow(2, 7.0 / 12.0));
my_sample.start();
} else { // Pad 4 released
Serial.println("t4 released");
}
break;
case 5:
if (pressed) { // Pad 5 pressed
Serial.println("t5 pressed");
my_sample.setFreq(default_freq * pow(2, 9.0 / 12.0));
my_sample.start();
} else { // Pad 5 released
Serial.println("t5 released");
}
break;
case 6:
if (pressed) { // Pad 6 pressed
Serial.println("t6 pressed");
my_sample.setFreq(default_freq * pow(2, 11.0 / 12.0));
my_sample.start();
} else { // Pad 6 released
Serial.println("t6 released");
}
break;
case 7:
if (pressed) { // Pad 7 pressed
Serial.println("t7 pressed");
my_sample.setFreq(default_freq * pow(2, 12.0 / 12.0));
my_sample.start();
} else { // Pad 7 released
Serial.println("t7 released");
}
break;
}
}
/**
* Runs whenever a DIP switch is toggled
*
* int number: the number (0-7) of the switch that was toggled
* bool up: true indicated switch was toggled up, false indicates switch was toggled
*/
void updateDip(int number, bool up) {
if (up) { // Any DIP toggled up
} else { //Any DIP toggled down
}
switch (number) {
case 0:
if (up) { // DIP 0 up
Serial.println("d0 up");
} else { // DIP 0 down
Serial.println("d0 down");
}
break;
case 1:
if (up) { // DIP 1 up
Serial.println("d1 up");
} else { // DIP 1 down
Serial.println("d1 down");
}
break;
case 2:
if (up) { // DIP 2 up
Serial.println("d2 up");
} else { // DIP 2 down
Serial.println("d2 down");
}
break;
case 3:
if (up) { // DIP 3 up
Serial.println("d3 up");
} else { // DIP 3 down
Serial.println("d3 down");
}
break;
case 4:
if (up) { // DIP 4 up
Serial.println("d4 up");
} else { // DIP 4 down
Serial.println("d4 down");
}
break;
case 5:
if (up) { // DIP 5 up
Serial.println("d5 up");
} else { // DIP 5 down
Serial.println("d5 down");
}
break;
case 6:
if (up) { // DIP 6 up
Serial.println("d6 up");
} else { // DIP 6 down
Serial.println("d6 down");
}
break;
case 7:
if (up) { // DIP 7 up
Serial.println("d7 up");
} else { // DIP 7 down
Serial.println("d7 down");
}
break;
}
}